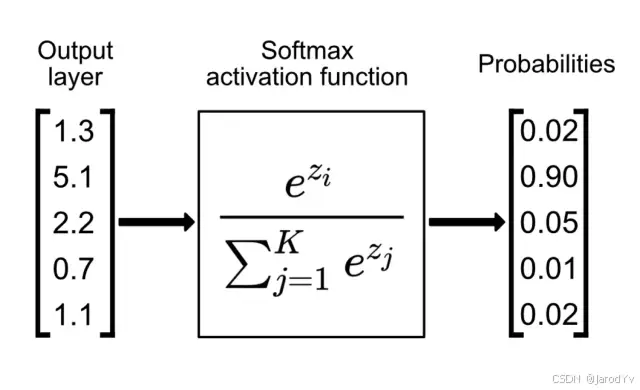
什么是 Softmax
Softmax 函数,又称归一化指数函数,它使用指数函数将输入向量归一化为概率分布(每一个元素的范围都在
(
0
,
1
)
(0,1)
(0,1) 之间,并且所有元素的和为
1
1
1)。Softmax 函数多用于多分类问题中。
Softmax 函数能够将一个包含
K
K
K 个实数值的向量
z
⃗
vec z
z “压缩”到另一个
K
K
K 个实数值的向量
σ
(
z
⃗
)
sigma(vec z)
σ(z),这些值的总和为
1
1
1。输入值可以是正数、负数、零或大于
1
1
1,但 Softmax 会将它们转换为
0
0
0 到
1
1
1 之间的值,以便可以解释为概率。如果某个输入值很小或为负,Softmax 会将其转换为小概率;如果输入值较大,则转换为大概率,但始终保持在
0
0
0 和
1
1
1 之间。
Softmax 是逻辑回归的一个泛化形式,可以用于多类分类,其公式与用于逻辑回归的 Sigmoid 函数非常相似。Softmax 函数只能在类别互斥时用于分类器。
在许多多层神经网络中,倒数第二层会输出一些未便于缩放的实数分数,这可能难以处理。在这种情况下,Softmax 很有用,因为它能够将这些分数转换为归一化的概率分布,既可以显示给用户,也可以作为其他系统的输入。因此,通常会将 Softmax 函数附加为神经网络的最终层。
Softmax 函数详解
Softmax 函数的定义如下:
| 公式 | 图像 |
|---|---|
|
σ ( z ⃗ ) i = e z i ∑ j = 1 K e z j qquad qquad qquad sigma(vec z)_i = frac{e^{z_i}}{sum_{j=1}^K e^{z_j}} qquad qquad qquad σ(z)i=∑j=1Kezjezi |
 |
输入是一个包含
K
K
K 个元素的向量
z
⃗
=
[
z
0
,
z
1
,
…
,
z
K
]
vec z = [z_0, z_1, dots, z_K]
z=[z0,z1,…,zK],其中不带箭头的
z
z
z 表示向量的一个元素。例如
z
⃗
=
[
2
,
3
,
5
,
8
]
→
{
z
1
=
2
z
2
=
3
x
3
=
5
z
4
=
8
vec z = [2,3,5,8] rarr begin{cases}z_1 = 2 \ z_2 = 3 \ x_3 = 5 \ z_4=8end{cases}
z=[2,3,5,8]→⎩
⎨
⎧z1=2z2=3x3=5z4=8
分子部分,Softmax 对向量的每个元素应用指数函数,对于最大的输入值返回最大的输出值。任何负数也变为正数,因为指数的值域为
(
0
,
∞
)
(0, infty)
(0,∞)。这可以通过查看指数函数的图像,或者通过检验下面的区间知晓。
(
e
−
∞
=
1
e
∞
=
0
,
e
∞
=
∞
)
Big(e^{-infty} = frac{1}{e^infty} = 0, e^infty = inftyBig)
(e−∞=e∞1=0,e∞=∞)
分母部分,Softmax 通过求和确保函数的总和为
1
1
1,从而将每个元素归一化,形成一个概率分布。所有经过指数化的元素会被加在一起,因此当每个指数化的元素除以这个总和时,它就表示为这个总和的一部分。例如
[
2
,
3
,
5
,
8
]
[2,3, 5, 8]
[2,3,5,8] 的指数化元素求和为:
∑
j
=
1
4
e
z
j
=
e
2
+
e
3
+
e
5
+
e
8
sum_{j=1}^4 e^{z_j} = e^2+e^3+e^5+e^8
j=1∑4ezj=e2+e3+e5+e8
示例
我们以
z
⃗
=
[
2
,
3
,
5
,
8
]
vec z = [2,3,5,8]
z=[2,3,5,8] 为例,演示 Softmax 的计算过程。
i
=
1
σ
(
z
⃗
)
1
=
e
2
e
2
+
e
3
+
e
5
+
e
8
=
0.00234
i
=
2
σ
(
z
⃗
)
2
=
e
3
e
2
+
e
3
+
e
5
+
e
8
=
0.00636
i
=
3
σ
(
z
⃗
)
3
=
e
5
e
2
+
e
3
+
e
5
+
e
8
=
0.04702
i
=
4
σ
(
z
⃗
)
4
=
e
8
e
2
+
e
3
+
e
5
+
e
8
=
0.94428
i=1 quad sigma(vec z)_1 = frac{e^2}{e^2+e^3+e^5+e^8} = 0.00234 \ i=2 quad sigma(vec z)_2 = frac{e^3}{e^2+e^3+e^5+e^8} = 0.00636 \ i=3 quad sigma(vec z)_3 = frac{e^5}{e^2+e^3+e^5+e^8} = 0.04702 \ i=4 quad sigma(vec z)_4 = frac{e^8}{e^2+e^3+e^5+e^8} = 0.94428
i=1σ(z)1=e2+e3+e5+e8e2=0.00234i=2σ(z)2=e2+e3+e5+e8e3=0.00636i=3σ(z)3=e2+e3+e5+e8e5=0.04702i=4σ(z)4=e2+e3+e5+e8e8=0.94428
最终输出为
[
0.00234
,
0.00636
,
0.04702
,
0.94428
]
[0.00234, 0.00636, 0.04702, 0.94428]
[0.00234,0.00636,0.04702,0.94428],所有元素之和为
1
1
1。最小的输入值
2
2
2 输出最小的概率;最大的输入值
8
8
8 输出最大的概率。
编程实现
Pytorch 中自带 Softmax 函数实现 nn.Softmax(),我们也可以根据 Softmax 函数的定义手动编程实现 Softmax 函数。
import torch
z = torch.Tensor([2, 3, 5, 8])
softmax = torch.exp(z) / torch.sum(torch.exp(z))
tensor([0.0023, 0.0064, 0.0470, 0.9443])
对矩阵应用 Softmax 函数
对矩阵应用 Softmax 并不是很多人想当然的那样,将每一个元素的指数除以所有元素的指数和,而是每个元素只与自己所在得向量进行 Softmax 运算。具体来说,对于下面的矩阵
M
=
[
[
1
,
2
,
3
]
[
4
,
5
,
6
]
[
7
,
8
,
9
]
]
M=begin{bmatrix} [1, 2, 3] \ [4, 5, 6] \ [7, 8, 9] end{bmatrix}
M=
[1,2,3][4,5,6][7,8,9]
我们其实是一行一行地对每个向量应用 Softmax。
i
=
1
,
j
=
1
σ
(
M
)
1
,
1
=
e
1
e
1
+
e
2
+
e
3
=
0.0900
i
=
1
,
j
=
2
σ
(
M
)
1
,
2
=
e
2
e
1
+
e
2
+
e
3
=
0.2447
i
=
1
,
j
=
3
σ
(
M
)
1
,
3
=
e
3
e
1
+
e
2
+
e
3
=
0.6652
i
=
2
,
j
=
1
σ
(
M
)
2
,
1
=
e
4
e
4
+
e
5
+
e
6
=
0.0900
i
=
2
,
j
=
2
σ
(
M
)
2
,
2
=
e
5
e
4
+
e
5
+
e
6
=
0.2447
i
=
2
,
j
=
3
σ
(
M
)
2
,
3
=
e
6
e
4
+
e
5
+
e
6
=
0.6652
i
=
3
,
j
=
1
σ
(
M
)
3
,
1
=
e
7
e
7
+
e
8
+
e
9
=
0.0900
i
=
3
,
j
=
2
σ
(
M
)
3
,
2
=
e
8
e
7
+
e
8
+
e
9
=
0.2447
i
=
3
,
j
=
3
σ
(
M
)
3
,
3
=
e
9
e
7
+
e
8
+
e
9
=
0.6652
i=1, j=1 quad sigma(M)_{1,1} = frac{e^1}{e^1+e^2+e^3} = 0.0900 \ i=1, j=2 quad sigma(M)_{1,2} = frac{e^2}{e^1+e^2+e^3} = 0.2447 \ i=1, j=3 quad sigma(M)_{1,3} = frac{e^3}{e^1+e^2+e^3} = 0.6652 \ i=2, j=1 quad sigma(M)_{2,1} = frac{e^4}{e^4+e^5+e^6} = 0.0900 \ i=2, j=2 quad sigma(M)_{2,2} = frac{e^5}{e^4+e^5+e^6} = 0.2447 \ i=2, j=3 quad sigma(M)_{2,3} = frac{e^6}{e^4+e^5+e^6} = 0.6652 \ i=3, j=1 quad sigma(M)_{3,1} = frac{e^7}{e^7+e^8+e^9} = 0.0900 \ i=3, j=2 quad sigma(M)_{3,2} = frac{e^8}{e^7+e^8+e^9} = 0.2447 \ i=3, j=3 quad sigma(M)_{3,3} = frac{e^9}{e^7+e^8+e^9} = 0.6652 \
i=1,j=1σ(M)1,1=e1+e2+e3e1=0.0900i=1,j=2σ(M)1,2=e1+e2+e3e2=0.2447i=1,j=3σ(M)1,3=e1+e2+e3e3=0.6652i=2,j=1σ(M)2,1=e4+e5+e6e4=0.0900i=2,j=2σ(M)2,2=e4+e5+e6e5=0.2447i=2,j=3σ(M)2,3=e4+e5+e6e6=0.6652i=3,j=1σ(M)3,1=e7+e8+e9e7=0.0900i=3,j=2σ(M)3,2=e7+e8+e9e8=0.2447i=3,j=3σ(M)3,3=e7+e8+e9e9=0.6652
用代码实现就是
x = torch.Tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
softmax = torch.exp(x) / torch.sum(torch.exp(x), axis=1, keepdims=True)
其中 axis=1 表示按行求和,keepdims = True 用于保持矩阵的形状。输出结果如下:
tensor([[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652]])
上面的输出,每一行相加的都等于
1
1
1。有趣的是输出结果中三个向量的值是相同的,这完全是巧合,因为
σ
(
M
)
1
,
1
=
e
1
e
1
+
e
2
+
e
3
=
e
e
(
1
+
e
+
e
2
)
=
1
1
+
e
+
e
2
σ
(
M
)
2
,
1
=
e
4
e
4
+
e
5
+
e
6
=
e
4
e
4
(
1
+
e
+
e
2
)
=
1
1
+
e
+
e
2
σ
(
M
)
3
,
1
=
e
7
e
7
+
e
8
+
e
9
=
e
7
e
7
(
1
+
e
+
e
2
)
=
1
1
+
e
+
e
2
sigma(M)_{1,1} = frac{e^1}{e^1+e^2+e^3} = frac{e}{e(1+e+e^2)} = frac{1}{1+e+e^2}\ sigma(M)_{2,1} = frac{e^4}{e^4+e^5+e^6} = frac{e^4}{e^4(1+e+e^2)} = frac{1}{1+e+e^2}\ sigma(M)_{3,1} = frac{e^7}{e^7+e^8+e^9} = frac{e^7}{e^7(1+e+e^2)} = frac{1}{1+e+e^2}\
σ(M)1,1=e1+e2+e3e1=e(1+e+e2)e=1+e+e21σ(M)2,1=e4+e5+e6e4=e4(1+e+e2)e4=1+e+e21σ(M)3,1=e7+e8+e9e7=e7(1+e+e2)e7=1+e+e21
再实际开发中,我们不会自己实现 Softmax 函数,而是直接调用 Pytorch 库自带的 nn.Softmax() 函数。
import torch.nn as nn
x = torch.Tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
softmax_layer = nn.Softmax(dim=1)
output = softmax_layer(x)
tensor([[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652],
[0.0900, 0.2447, 0.6652]])

评论(0)